26 March 2016
Liquid Types
Authors: Rondon, Kawaguchi, Jhala
Conference: PLDI 2008
Functional programming languages provide type systems that ensure invariants on programs at compile-time. To obtain even finer properties captured by types, several authors have proposed to adopt dependent types as a way to improve expressivity of type systems. Unfortunately, type inference needs considerable programmers’ guidance by means of type annotations. Liquid types provide an exciting compromise.
Type systems are a fundamental piece of modern functional programming languages like Haskell or OCaml. In particular, Hindley-Milner inspired type systems main features are strong static typing, that allows to capture (some) errors at compile-time, and type inference, that alleviates programmers’ burden in annotating programs with type information.
Type systems allow to encode program invariants by means of types. Lately,
dependent types have been introduced in order to express even finer
properties on programs. As an example, classic type systems can express the
fact that a variable i has type int (written \(i : int\)), i.e. i
is always an integer, while dependent type systems may refine this into
\(i : \left[ \nu : int\ |\ 0 \leq \nu \leq 99\right]\) telling that the
actual values taken by i are integers between 0 and 99. There is a
problem though: dependent types make type inference undecidable in
general. In practice, this means that programmers are back to a system
needing a lot of type annotations (the authors cite benchmarks of Pfenning
and Xi’s work on DML where 31% of the code is manual annotations for
ensuring safety).
Logically qualified data types, or simply liquid types, are an interesting compromise. The system provides “[…] many of the benefits of dependent types […] without the heavy price of manual annotation” by extendind the Hindley-Milner type inference algorithm with a predicate abstraction-like technique (or fixed-point computation), commonly used in model checking for synthesizing loop invariants.
Liquid types are dependent types of the form \(\left[ \nu : \tau\ |
\epsilon \right]\) (aka type refinement) where \(\nu \) is a special
value variable, \(\tau \) is a structural type, and \(\epsilon \) is
a refinement predicate. In particular, \(\epsilon \) is called a
logical qualifier which is a conjunction of boolean predicates over
\(\nu \), program variables, and a special placeholder for program
variables \(\star \).
It is important to stress that the system is parametrized over a set of logical qualifiers \(\mathbb{Q} \) as the inference algorithm reasons on them when solving typing constraints. The authors focus on the problem of safety for array accessing, and so they set \(\mathbb{Q}\) to be the set of logical qualifiers {\(0\leq \nu, \star\leq\nu, \nu\lt\star,\nu\lt\mathtt{len}\,\star\)}, where \(\mathtt{len\,a}\) is the function returning the length of \(\mathtt{a}\).
The main idea is a three-step algorithm for dependent type inference that is designed as follows:
- First, Hindley-Milner’s algorithm is invoked to obtain a structural type which is then turned into a so-called template, a dependent type with the same structure of the original one, but with liquid type variables representing unknown type refinements,
- Second, by following liquid type derivation rules, liquid type constraints are built in order to capture the subtyping relationships between the templates that must be met for a liquid type derivation to exist,
- Third, subtyping derivation rules gives a way to split subtyping constraints into simple constraints over liquid type variables, finally solved by performing a fixed point computation over logical qualifiers \(\mathbb{Q} \) that may involve the use of a solver.
An informal presentation of the inference algorithm at work is given for the function:
let max x y =
if x > y then x else y
First, Hindley-Milner’s algorithm on max returns \( x:int \rightarrow
y:int \rightarrow int\), then generating the template \(x
:\mathcal{k_{x}} \rightarrow y:\mathcal{k_{y}} \rightarrow
\mathcal{k}\), where \(\mathcal{k_{x}}, \mathcal{k_{y}}\) and
\(\mathcal{k}\) are liquid type variables representing the unknown
refinements for the formals x, y and the body of max
respectively. Second, since the body of max is an if-then-else
expression, the algorithm generates the following two constraints that
capture the result subtyping relations with respect to branching
conditions (path-sensitivity property):
- \(x:\mathcal{k_{x}};y:\mathcal{k_{y}};(x\gt y)\vdash \left[\nu = x\right]<:\mathcal{k}\)
- \(x:\mathcal{k_{x}};y:\mathcal{k_{y}};(x\leq y)\vdash \left[\nu = y\right]<:\mathcal{k}\)
These constraints tell that, when \(x\gt y\) (resp. \(x\leq y\)), then
the type of the resulting expression \(x\) (resp. \(y\)) must be a
subtype of the body type \(\mathcal{k}\). Third, since the program does
not particularly use x and y, the inference algorithm assigns
\(\mathcal{k_{x}},\mathcal{k_{y}}\) the value \(true\) (i.e. any
integer may be passed in). On result subtyping constraints, a solver is
used to find the strongest conjunction of logical qualifiers in
\(\mathbb{Q}^\star\) (i.e. instantiation of \(\mathbb{Q}\) on formal
program variables). At the end, the system infers that \(\mathcal{k}\)
should be \((x\leq\nu)\wedge (y\leq\nu)\), hence
\[
max : x:int\rightarrow y:int\rightarrow\left[\nu : int\ |
(x\leq\nu)\wedge (y\leq\nu)\right].
\]
In particular, subtyping constraints like \(\left[\nu =
x\right]<:\mathcal{k}\) and \(\left[\nu = y\right]<:\mathcal{k}\) are
finally solved by performing a fixed point computation over
\(\mathbb{Q}^\star\) (typically, liquid type variable take the conjuction of every
possible qualifiers over formal variables, then weakened at every
iteration of the computation) and using the “[…] conservative but
decidable implication check” 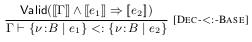 .
Here \([[ e]]\) stands for the embedding of the expression \(e\) into
terms of a decidable logic of equality, uninterpreted functions and
linear arithmetic. Such a logic is commonly solved by SMT solvers like
Z3.
.
Here \([[ e]]\) stands for the embedding of the expression \(e\) into
terms of a decidable logic of equality, uninterpreted functions and
linear arithmetic. Such a logic is commonly solved by SMT solvers like
Z3.
The authors explain that inference becomes decidable because, intuitively, the space of possible types remains bounded thanks to the following three observations:
- “[…] a conservative but decidable notion of subtyping, where we reduce the subtyping of arbitrary dependent types to a set of implication checks over base types, each of which is deemed to hold if and only if an embeddings of the implication into a decidable logic yields a valid formula in the logic”,
- “[…] an expression has a valid liquid type derivation only if it has a valid ML type derivarion, and the dependent type of every subexpression is a refinement of its ML type”,
- “[…] the type of certain expressions, such as
\(\lambda\)-abstractions,
if-then-elseexpressions, and recursive functions must be liquid”.
The authors prove the following main properties about their inference algorithm Infer:
- \(\mathtt{Infer}(\Gamma,e,\mathbb{Q})\) terminates,
- If \(\mathtt{Infer}(\Gamma,e,\mathbb{Q})=S\) then \(\Gamma\vdash_{\mathbb{Q}} e:S\),
- If \(\mathtt{Infer}(\Gamma,e,\mathbb{Q})=Failure\) then there is no \(S\) s.t. \(\Gamma\vdash_{\mathbb{Q}} e:S\).
The third statements is about programs that do not typecheck. Indeed, each instantiation of the system is complete, but still “[…] there may be safe programs which cannot be well-typed […] due to either an inappopriate choice of qualifiers or the conservativeness of our notion of subtyping. In the former case, we can […] manually add more qualifiers, and in the latter […] insert a minimal set of run-time checks.”.
The authors conclude with benchmarks, stressing the owesome outcome that, on average, liquid types need only 1% of program text for type annotations.
