20 March 2016
Equality Saturation: a New Approach to Optimization
Authors: Tate, Stepp, Tatlock, Lerner
Conference: POPL 2009
A common challenge in optimizing compilers is the phase ordering problem: in which order should different optimizations be applied? The problematic issue is that applying one optimization may change the program such that some other, potentially more profitable, optimization can no longer be performed. Equality saturation is a clever idea for getting around the phase ordering problem. As an interesting side effect, an optimizer based on equality saturation can also be used for translation validation of other optimizers.
Consider the expression i * 5 where i is an integer. Multiplication
instructions commonly take several CPU cycles, so compilers try to optimize
such multiplications by constants to cheaper expressions. In this particular
case, i << 2 + i computes the same value, but many processors can do the
shift and the add in a single instruction that executes in fewer cycles than
the original multiplication. Thus this replacement is an optimization.
Now consider the same expression in context, as part of a larger piece of code:
i := 0;
while (...) {
use(i * 5);
i := i + 1;
...
}
(This is a simplified version of the running example in the original paper. All omissions, misunderstandings, and other errors are entirely my fault, not the original authors’.)
This pattern of accesses to i allows the compiler perform an optimization
known as strengh reduction, replacing the “strong” multiplication
operation by “weaker” additions:
i := 0;
while (...) {
use(i);
i := i + 5;
...
}
This version is equivalent to the original, passing the values 0, 5, 10, …
to the use operation. However, it uses a single addition per loop
iteration, which is faster than both the variant with the multiplication and
the variant where i * 5 is replaced by i << 2 + i.
We have seen that two optimizations apply to this piece of code and that one
is better than the other. The phase ordering problem arises when, for some
reason, the compiler applies the “less useful” optimization first: If we
replace i * 5 by i << 2 + i, the code becomes obfuscated, and the
compiler may no longer be able to detect that this is equivalent to a simple
multiplication. It may thus have prevented itself from applying the more
powerful strength reduction transformation.
This is where this paper’s equality saturation optimization comes
in. The basic idea is simple: when finding opportunities for optimization,
do not apply them destructively but simply record the information that
some other variant of the program is equivalent to the existing one. So in
the example, the optimizer would never replace i * 5 by i << 2 + i
but only add these expressions to the same equivalence class.
The optimizer works on a representation of programs as program expression graphs (PEGs). This is a kind of cyclic data dependence graph with special θ nodes to represent loops. Here is a PEG for the looping program above:
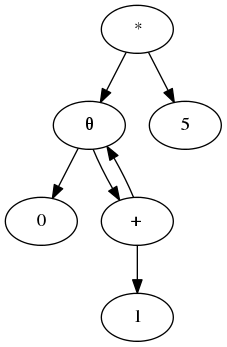
The θ node represents the sequence of values that an expression takes in a
loop. On the first iteration, it has the value of the first argument; on
subsequent iterations, the second (recursive) argument is evaluated to yield
the next value. In the example graph, the θ represents the value of i on
subsequent iterations: 0, 1, 2, …; the multiplication by 5 yields the
values for i * 5: 0, 5, 10, … .
This graph can be extended to an E-PEG (PEG with equalities) by adding more nodes and using dashed equivalence edges to connect nodes that represent the same values. Here is the extended graph that we get by optimizing the multiplication by 5:
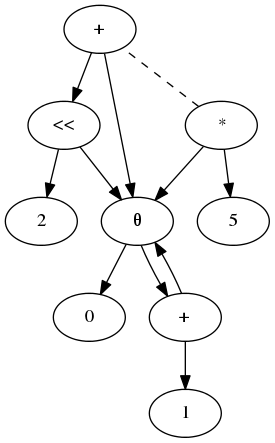
(In this graphical representation the order of the operands of the shift operation is mixed up. The price I pay for simplifying the paper’s example is having to re-draw their graphs, and for a blog post I believe this is about good enough.)
The dashed edge connecting the two root nodes expresses the fact that i *
5 and i << 2 + i represent the same value.
The key point here is that applying this transformation only added information to the graph but did not destroy anything. If some optimization applied before, it still applies. Thus in this setting we can still perform strength reduction on the original loop because the other optimization did not destroy it.
In equality saturation, optimizations are expressed by
equality axioms. Simple strength reduction can be expressed by the
combination of the axioms (a + b) * m = a * m + b * m (distributivity of
multiplication over addition) and θ(a, b) * m = θ(a * m, b * m)
(distributivity of multiplication over θ). Whenever a node in the PEG
matches one side of an equation, we may add a node representing the other
side and connect the two by an equality edge. This explains the name of the
approach, equality saturation: Starting with a graph, equalities are
applied until the graph is saturated in that nothing more can (or should)
be added. In practice, the growth of the graph must be limited to avoid
uncontrollable blow-up.
Applying the two axioms above yields the following graph:
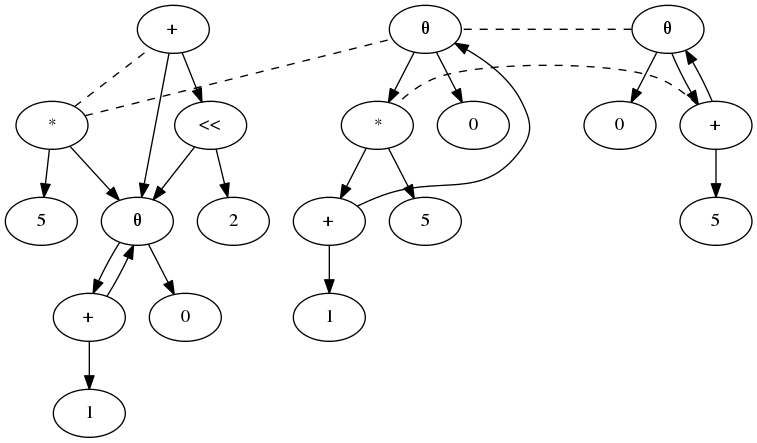
After the saturation step, the graph represents not one but many equivalent programs. The actual “optimization” consists of picking the best of these many variants. This amounts to choosing a minimal-cost subset of the nodes that together make up one of the variants. The authors encode this step as a 0-1 integer linear program and use an external solver to find a solution of minimal cost. The cost model assigns weights to nodes by operation type such that, for example, multiplications are more expensive than additions. In the running example, the solver would pick the rightmost subgraph which corresponds directly to the pseudocode after strength reduction given above.
As the authors observe, this optimization approach can also be used to perform translation validation, i.e., to ensure that the transformations performed by another optimizer are indeed valid. To perform validation, observe the original program that goes into an optimizer as well as its output, an allegedly equivalent program. Build the saturated E-PEG for the original program, yielding a representation of a large set of equivalent variants. Now, if the optimizer’s output is contained, in the E-PEG, the translation is indeed valid. Otherwise, the optimizer may have a bug; alternatively, however, the equality saturation may have been incomplete. This can be the case either because the saturation process was stopped too early, or because the set of underlying axioms is incomplete.
The authors discuss an evaluation of equality saturation for interprocedural optimization of Java bytecode. They compare their tool, Peggy, with the Soot optimization framework. They found that both optimizers give comparable results in general. However, Peggy allows users to easily specify domain-specific optimizations by adding axioms to its database; on some small examples, this allows significant speedups. Running in translation validation mode, Peggy was able to validate 98% of Soot’s interprocedural optimizations on a large benchmark set. Examining the remaining cases, they uncovered a bug in Soot that led to incorrectly optimized code.
Overall, equality saturation is a fascinating idea for structuring compilers. Unfortunately, the costs seem to prohibit its use in real-world compilers in mainstream settings.
(article written by GB)
